纳什博弈是自我强制的，每个人都相信自己会赞同协议。

领导力可以在协调博弈中将人调到一个特定的平衡。

战略补充博弈:类似协调博弈，双方都想做的更多

Game One:

Going to the Moive博弈：收益为想要看某部电影的欲望

所以电影三是受控策略，严格劣势策略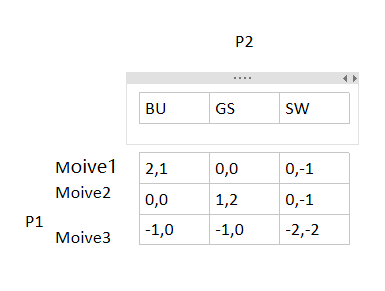

BR1==BR2==(movie1) and (movie2)

最佳反应和纳什均衡相同，但是两种均衡冲突

Battle of the sex:指的是不同的人想要不同的协调结果的协调博弈

古诺双寡头模型：一种古典模型

在于如果玩家很少，策略也很少的情况下怎么找到纳什均衡。

Game Two

比如市场是两个公司竞争，可能达到两种情况，垄断或者激烈竞争。

有两点注意：一者是意识市场上将要发生什么，二者是站在福利或者政府角度，考虑它对消费者或者生成商是否有利，这个哈利益以及消费者过剩有关联。

Player: 2 firms

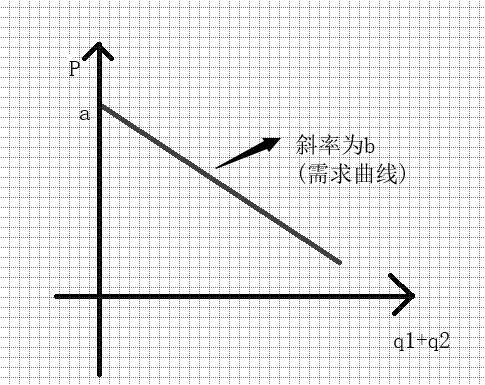
Strategy :每个公司都生产某种特定产品，消费者可以互换这两个产品

使用q代表数量策略

Cost: c代表成本，固定的边缘成本,

Price: P=a-b(q1+q2), 其中q1和q2是公司生产的总数量,需求曲线的斜率为b

Pay off:公司的目标是最大化利润，Firm1= priceq1-costq1=aq1-bq1q1-bq1q2-cq1(将price带入公式)

FIrm2=aq2-bq1q1-bq1q2-cq2.

怎么找到纳什均衡？找到彼此的最佳反应集合，判断交集。

在这个博弈里最佳反应就是利润最大化了，所以对上述的利润公式求导，找到最大值即可，定义域为各自的产品数量。

Firm1: 此时q1为自变量，所以为q1求导，得到F'=a-2bq1-bq2-c,令其为0.再求导得到F''=-2b<0,所以为极大值点，所以BR1(q2)=q1'=(a-c)/2b-q2/2,是个关于q2的函数，解得Br1(0)=(a-c)/2b,即垄断产量，q2=0时q1的产量，在边际收益等于边际成本的地方。

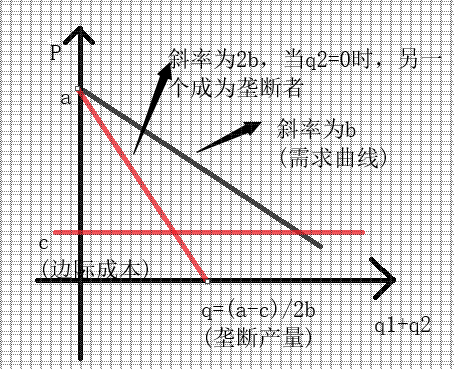
BR1=0,得到q2=(a-c)/b，此时q1=0,公司1将不会生产，话句话说，仅仅靠q2的产量，价格就已经下跌到成本了，再生产也不会有什么收益，可能还会使得价格降至成本以下，就会亏损。

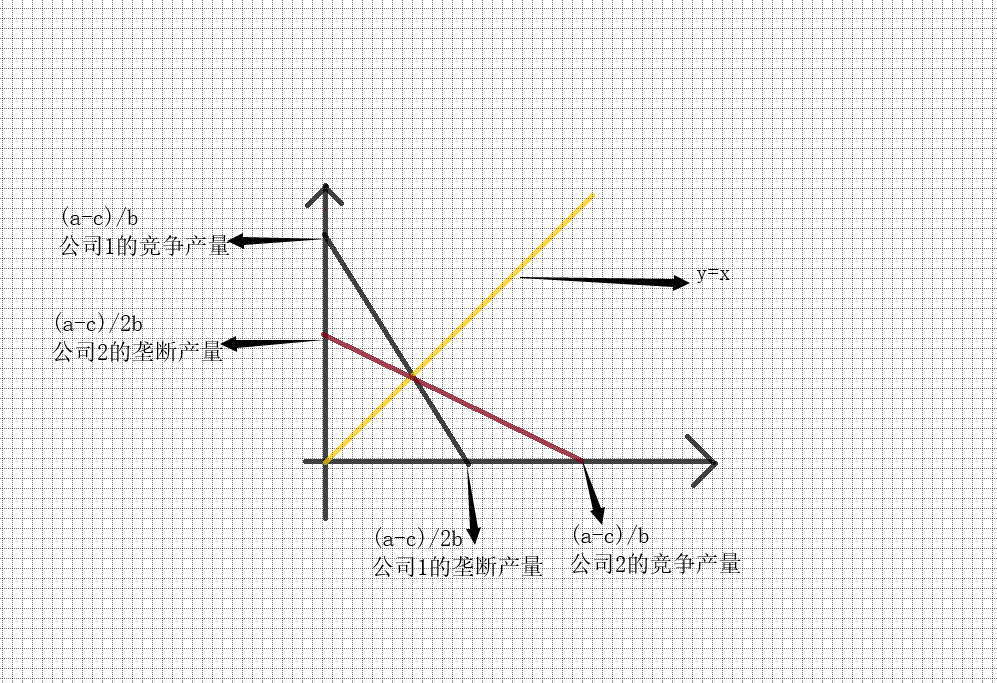
这个需求等于边际成本的产量，叫做完全竞争产量。

同理可以得到BR2(q1)=q2'=(a-c)/2b-q1/2，是个关于q1的函数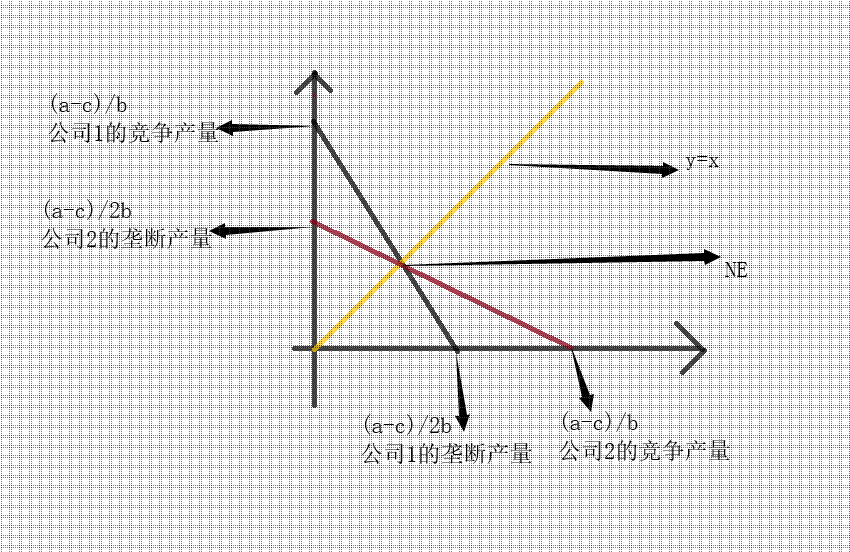

如图所示，可以得到NE,即q1'=q2'

所以联立两个式子得到q1'=(a-c)/3b=q2',这个产量为古诺产量

这个和合作博弈，投资博弈博弈不同的是，玩家间是对立的，利益相驳

在两个垄断产量点可以保证利润，但是如果两个(不完全竞争)公司想要合作垄断(仅限数量竞争时)的时候，其他的竞争者会蜂拥而至加入这个行业，再次导致利润下降。